【手性对称性定义】

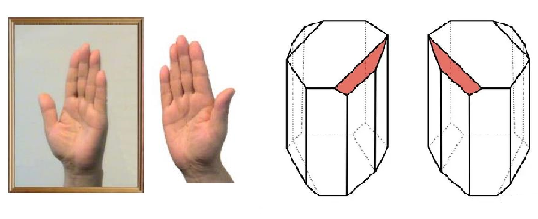
 手性对称性: 如果两个几何图形互成镜像，但它们不能用平移、旋转和反射等方法重合在一起，则称这两个图形是手性对称的。手性对称性的最典型例子是人的左手和右手。每个人都有两只手，镜外的观察者看到右手在平面镜中的像是左手，不难想象，左手在平面镜中的像必然是右手，它们互为镜像。左手和右手的形状和大小完全相同，但是你可以用平移或转动的方法将两只手完全重合起来吗？不能。如果使用反射的方法，把两只手合起来，虽然手心和手心重合在一起，但手背和手背却没有重合在一起，所以还是不能把两只手重合在一起。即使组合运用几种对称性操作，也不能使它们重合在一起。我们由此得出结论：右手不能与右手的镜像重合，左手也不能与左手的镜像重合；右手只能和左手的镜像完全重合在一起，左手只能和右手的镜像完全重合在一起。左手和右手的这种对称性就是手性对称性。

与此类似，任何两个呈镜像对称却不能重合的三维物体，就具有手性对称性。当然，化学上有机分子因构造相同而构型不同的分子，就会呈现镜像对称却不重合的手性对称性。这样相互对映的有机分子，我们叫它们为对映异构体。对映异构体具有旋光性，可分为左旋和右旋对映体，所以也叫做旋光异构体。

                                                            丰都智愚河畔环境技术工作室